Graphical Models-Bayesian Belief Networks, Markov Random Fields(MRFs)

Probabilities play a central role in modern pattern recognition.it highly advantageous to augment the analysis using diagrammatic representations of probability distributions, called probabilistic graphical models. These offer several useful properties

1. They provide a simple way to visualize the structure of a probabilistic model and can be used to design and motivate new models.

2. Insights into the properties of the model, including conditional independence properties, can be obtained by inspection of the graph.

3. Complex computations, required to perform inference and learning in sophisticated models, can be expressed in terms of graphical manipulations, in which underlying mathematical expressions are carried along implicitly.

A graph comprises nodes (also called vertices) connected by links (also known as edges or arcs). In a probabilistic graphical model, each node represents a random variable (or group of random variables), and the links express probabilistic relationships between these variables. The graph then captures the way in which the joint distribution over all of the random variables can be decomposed into a product of

factors each depending only on a subset of the variables. We shall begin by discussing Bayesian networks, also known as directed graphical models, in which the links of the graphs have a particular directionality indicated by arrows. The other major class of graphical models are Markov random fields, also known as undirected graphical models, in which the links do not carry arrows and have no directional significance. Directed graphs are useful for expressing causal relationships between random variables, whereas undirected graphs are better suited to expressing soft constraints between random variables. For the purposes of solving inference problems, it is often convenient to convert both directed and undirected graphs into a different representation called a factor graph.

In this , we shall focus on the key aspects of graphical models as needed for applications in pattern recognition and machine learning.

Bayesian Networks Judea Pearl (1988),

Bayesian belief network is key computer technology for dealing with probabilistic events and to solve a problem which has uncertainty. We can define a Bayesian network as:

"A Bayesian network is a probabilistic graphical model which represents a set of variables and their conditional dependencies using a directed acyclic graph."

It is also called a Bayes network, belief network, decision network, or Bayesian model.

Bayesian networks are probabilistic, because these networks are built from a probability distribution, and also use probability theory for prediction and anomaly detection.

Bayesian networks provide useful benefits as a probabilistic model.For example:

Visualization. The model provides a direct way to visualize the structure of the model and motivate the design of new models.

Relationships. Provides insights into the presence and absence of the relationships between random variables.

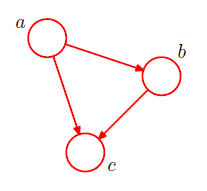
Computations. Provides a way to structure complex probability calculations.

In order to motivate the use of directed graphs to describe probability distributions, consider first an arbitrary joint distribution $p(a, b, c)$ over three variables $a, b,$ and $c$. Note that at this stage, we do not need to specify anything further about these variables, such as whether they are discrete or continuous. Indeed, one of the powerful aspects of graphical models is that a specific graph can make probabilistic statements for a broad class of distributions. By application of the product rule of probability  we can write the joint distribution in the form

$p(a, b, c) = p(c|a, b)p(a, b).$

A second application of the product rule, this time to the second term on the righthand side of , gives

$p(a, b, c) = p(c|a, b)p(b|a)p(a)$.

Note that this decomposition holds for any choice of the joint distribution. We now represent the right-hand side of  in terms of a simple graphical model as follows. First we introduce a node for each of the random variables $a$, $b$, and $c$ and associate each node with the corresponding conditional distribution on the right-hand side of above equation.Then, for each conditional distribution we add directed links (arrows) to the graph from the nodes corresponding to the variables on which the distribution is conditioned. Thus for the factor $p(c|a, b)$, there will be links from nodes $a$ and $b$ to node $c$, whereas for the factor $p(a)$ there will be no incoming links. The result is the graph shown in Figure below.

If there is a link going from a node $a$ to a node $b$, then we say that node $a$ is the parent of node $b$, and we say that node $b$ is the child of node $a$.Note that we shall not make any formal distinction between a node and the variable to which it corresponds but will simply use the same symbol to refer to both.We have implicitly chosen a particular ordering, namely $a, b, c$, and had we chosen a different ordering we would have obtained a different decomposition and hence a different graphical representation.

For the moment let us extend the example  by considering the joint distribution over $K$ variables given by $p(x_1, . . . , x_K)$. By repeated application of the product rule of probability, this joint distribution can be written as a product of conditional distributions, one for each of the variables

$p(x_1, . . . , x_K) = p(x_K|x_1, . . . , x_{K−1}) . . . p(x_2|x_1)p(x_1).$

For a given choice of $K$, we can again represent this as a directed graph having $K$ nodes, one for each conditional distribution on the right-hand side of above eqn, with each node having incoming links from all lower numbered nodes. We say that this graph is fully connected because there is a link between every pair of nodes.

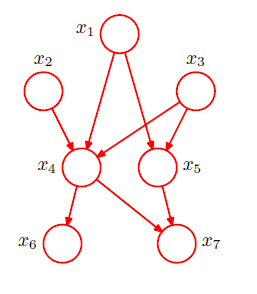
Consider the graph shown below. This is not a fully connected graph because, for instance, there is no link from $x_1$ to $x_2$ or from $x_3$ to$x_7$. The graph and the corresponding decomposition of the joint probability is given by

We can now state in general terms the relationship between a given directed graph and the corresponding distribution over the variables. The joint distribution defined by a graph is given by the product, over all of the nodes of the graph, of a conditional distribution for each node conditioned on the variables corresponding to the parents of that node in the graph. Thus, for a graph with $K$ nodes, the joint distribution is given by

$p(x)=\prod_{k=1}^K p(x_k|pa_k)$

where $pa_k$ denotes the set of parents of $x_k$, and $x = \{x_1, . . . , x_K\}$. This key equation expresses the factorization properties of the joint distribution for a directed graphical model. Although we have considered each node to correspond to a single variable, we can equally well associate sets of variables and vector-valued variables with the nodes of a graph.

The directed graphs that we are considering are subject to an important restriction namely that there must be no directed cycles, in other words there are no closed paths within the graph such that we can move from node to node along links following the direction of the arrows and end up back at the starting node. Such graphs are  also called directed acyclic graphs, or DAGs. This is equivalent to the statement that there exists an ordering of the nodes such that there are no links that go from any node to any lower numbered node.

The Bayesian network graph does not contain any cyclic graph. Hence, it is known as a directed acyclic graph or DAG.

Example:

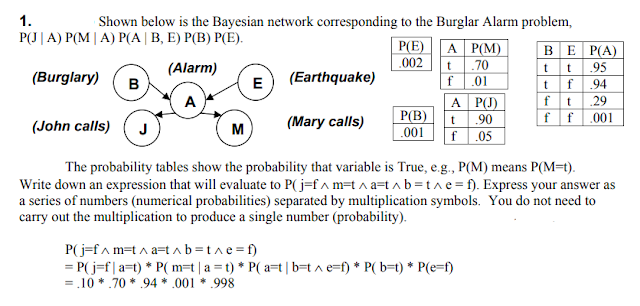
Harry installed a new burglar alarm at his home to detect burglary. The alarm reliably responds at detecting a burglary but also responds for minor earthquakes. Harry has two neighbors David and Sophia, who have taken a responsibility to inform Harry at work when they hear the alarm. David always calls Harry when he hears the alarm, but sometimes he got confused with the phone ringing and calls at that time too. On the other hand, Sophia likes to listen to high music, so sometimes she misses to hear the alarm. Here we would like to compute the probability of Burglary Alarm.

Problem:

Calculate the probability that alarm has sounded, but there is neither a burglary, nor an earthquake occurred, and David and Sophia both called the Harry.

Solution:

The Bayesian network for the above problem is given below. The network structure is showing that burglary and earthquake is the parent node of the alarm and directly affecting the probability of alarm's going off, but David and Sophia's calls depend on alarm probability.

The network is representing that our assumptions do not directly perceive the burglary and also do not notice the minor earthquake, and they also not confer before calling.

The conditional distributions for each node are given as conditional probabilities table or CPT.

Each row in the CPT must be sum to 1 because all the entries in the table represent an exhaustive set of cases for the variable.

In CPT, a boolean variable with $k$ boolean parents contains $2^K$ probabilities. Hence, if there are two parents, then CPT will contain 4 probability values

List of all events occurring in this network:

Burglary (B)
Earthquake(E)
Alarm(A)
David Calls(D)
Sophia calls(S)

We can write the events of problem statement in the form of probability: $P[D, S, A, B, E]$, can rewrite the above probability statement using joint probability distribution:

$P[D, S, A, B, E]= P[D | S, A, B, E]. P[S, A, B, E]$

$=P[D | S, A, B, E]. P[S | A, B, E]. P[A, B, E]$

$= P [D| A]. P [ S| A, B, E]. P[ A, B, E]$

$= P[D | A]. P[ S | A]. P[A| B, E]. P[B, E]$

$= P[D | A ]. P[S | A]. P[A| B, E]. P[B |E]. P[E]$

From the formula of joint distribution, we can write the problem statement in the form of probability distribution:

$P(S, D, A, ¬B, ¬E) = P (S|A) *P (D|A)*P (A|¬B ^ ¬E) *P (¬B) *P (¬E).$

$= 0.75* 0.91* 0.001* 0.998*0.999$

$= 0.00068045.$

Hence, a Bayesian network can answer any query about the domain by using Joint distribution.

The semantics of Bayesian Network:

There are two ways to understand the semantics of the Bayesian network, which is given below:

1. To understand the network as the representation of the Joint probability distribution.It is helpful to understand how to construct the network.

2. To understand the network as an encoding of a collection of conditional independence statements.It is helpful in designing inference procedure.

Markov Random Fields

A Markov random field, also known as a Markov network or an undirected graphical model (Kindermann and Snell, 1980), has a set of nodes each of which corresponds to a variable or group of variables, as well as a set of links each of which connects a pair of nodes. The links are undirected, that is they do not carry arrows. 

A Markov network is similar to a Bayesian network in its representation of dependencies; the differences being that Bayesian networks are directed and acyclic, whereas Markov networks are undirected and may be cyclic. Thus, a Markov network can represent certain dependencies that a Bayesian network cannot. On the other hand, it can’t represent certain dependencies that a Bayesian network can (such as induced dependencies). The underlying graph of a Markov random field may be finite or infinite

In the case of undirected graphs, it is convenient to begin with a discussion of conditional independence properties.

An example of a Markov random field. Each edge represents dependency. In this example: $A$ depends on $B$ and $D$. $B4 depends on $A$ and $D$. $D$ depends on $A, B$, and $E$. $E$ depends on $D$ and $C$. $C$ depends on $E$.

Conditional independence properties

 In the case of directed graphs, we saw that it was possible to test whether a particular conditional independence property holds by applying a graphical test called d-separation. This involved testing whether or not the paths connecting two sets of nodes were ‘blocked’. The definition of blocked, however, was somewhat subtle due to the presence of paths having head-to-head nodes. We might ask whether it is possible to define an alternative graphical semantics for probability distributions such that conditional independence is determined by simple graph separation. This is indeed the case and corresponds to undirected graphical models. By removing the directionality from the links of the graph, the asymmetry between parent and child nodes is removed, and so the subtleties associated with head-to-head nodes no longer arise. Suppose that in an undirected graph we identify three sets of nodes, denoted $A$,$B$, and $C$, and that we consider the conditional independence property

$A ⊥⊥ B | C$

To test whether this property is satisfied by a probability distribution defined by a graph we consider all possible paths that connect nodes in set $A$ to nodes in set $B$. If all such paths pass through one or more nodes in set $C$, then all such paths are ‘blocked’ and so the conditional independence property holds. However, if there is at least one such path that is not blocked, then the property does not necessarily hold, or more precisely there will exist at least some distributions corresponding to the graph that do not satisfy this conditional independence relation. This is illustrated with an example in Figure below. Note that this is exactly the same as the d-separation criterion except that there is no ‘explaining away’ phenomenon. Testing for conditional independence in undirected graphs is therefore simpler than in directed graphs.

An alternative way to view the conditional independence test is to imagine removing all nodes in set $C$ from the graph together with any links that connect to those nodes. We then ask if there exists a path that connects any node in $A$ to any node in $B$. If there are no such paths, then the conditional independence property must hold.

The Markov blanket for an undirected graph takes a particularly simple form, because a node will be conditionally independent of all other nodes conditioned only on the neighbouring nodes, as illustrated in Figure.

Factorization properties cliques

We now seek a factorization rule for undirected graphs that will correspond to the above conditional independence test. Again, this will involve expressing the joint distribution $p(x)$ as a product of functions defined over sets of variables that are local to the graph. We therefore need to decide what is the appropriate notion of locality in this case.

If we consider two nodes $x_i$ and $x_j$ that are not connected by a link, then these variables must be conditionally independent given all other nodes in the graph. This follows from the fact that there is no direct path between the two nodes, and all other paths pass through nodes that are observed, and hence those paths are blocked. This conditional independence property can be expressed as

$p(x_i, x_j |x' \{i,j\}) = p(x_i|x' \{i,j\})p(x_j |x' \{i,j\})$

where $x' \{i,j\}$ denotes the set $x$ of all variables with $x_i$ and $x_j$ removed. The factorization of the joint distribution must therefore be such that $x_i$ and $x_j$ do not appear in the same factor in order for the conditional independence property to hold for all possible distributions belonging to the graph.

This leads us to consider a graphical concept called a clique, which is defined as a subset of the nodes in a graph such that there exists a link between all pairs of nodes in the subset. In other words, the set of nodes in a clique is fully connected. Furthermore, a maximal clique is a clique such that it is not possible to include any other nodes from the graph in the set without it ceasing to be a clique

This graph has five cliques of two nodes given by $\{x1, x2\}, \{x2, x3\}, \{x3, x4\}, \{x4, x2\}$,and  $\{x1, x3\}$, as well as two maximal cliques given by $\{x1, x2, x3\}$ and $\{x2, x3, x4\}$.The set $\{x1, x2, x3, x4\}$ is not a clique because of the missing link from $x1$ to $x4$. We can therefore define the factors in the decomposition of the joint distribution to be functions of the variables in the cliques. In fact, we can consider functions of the maximal cliques, without loss of generality, because other cliques must be subsets of maximal cliques. Thus, if $\{x1, x2, x3\}$ is a maximal clique and we define an arbitrary function over this clique, then including another factor defined over a subset of these variables would be redundant.

Let us denote a clique by $C$ and the set of variables in that clique by $x_C$. Then the joint distribution is written as a product of potential functions $ψ_C(x_C)$ over the maximal cliques of the graph

$p(x)=\frac{1}{Z}\prod_C \psi_C(x_C)$

Here the quantity $Z$, sometimes called the partition function, is a normalization constant and is given by

$Z=\sum_x \frac{1}{Z}\prod_C \psi_C(x_C)$

which ensures that the distribution $p(x)$ given by  is correctly normalized.By considering only potential functions which satisfy $ψ_C(x_C) \ge 0$ we ensure that $p(x) \ge 0$. In the eqn we have assumed that $x$ comprises discrete variables, but the framework is equally applicable to continuous variables, or a combination of the two, in which the summation is replaced by the appropriate combination of summation and integration.

Example:

More generally, MRFs have several advantages over directed models:

They can be applied to a wider range of problems in which there is no natural directionality associated with variable dependencies.

Undirected graphs can succinctly express certain dependencies that Bayesian nets cannot easily describe (although the converse is also true)

They also possess several important drawbacks:

Computing the normalization constant Z  requires summing over a potentially exponential number of assignments. We will see that in the general case, this will be NP-hard; thus many undirected models will be intractable and will require approximation techniques.

Undirected models may be difficult to interpret.

It is much easier to generate data from a Bayesian network, which is important in some applications.

It is not hard to see that Bayesian networks are a special case of MRFs with a very specific type of clique factor (one that corresponds to a conditional probability distribution and implies a directed acyclic structure in the graph), and a normalizing constant of one. In particular, if we take a directed graph $G$ and add side edges to all parents of a given node (and removing their directionality), then the CPDs (seen as factors over a variable and its ancestors) factorize over the resulting undirected graph. The resulting process is called moralization.

Example Problems

Write down the factored conditional probability expression that corresponds to the graphical Bayesian Network shown.

Soln:

$P(A | C,D,H) .P(B | D,E,G) P(C | F,I) P(D | G,H) P(E | J) P(F | I) P(G | H,J) P(H) P(I) P(J)$

Draw the Bayesian Network that corresponds to this conditional probability: $P(A | B,C,E) P(B | D,G) P(C | E,F,H) P(D | G) P(E| G,H) P(F | I) P(G | H) P(H | I) P(I)$